2025年云南公務員考試行測技巧:數量關系中的極值問題怎么解
 更多行測技巧與方法掃碼獲取
更多行測技巧與方法掃碼獲取
數量關系中的極值問題怎么解
極值問題在近幾年的行測數量關系考試中都有涉及,是公考中較為常見的題型,其中以和定最值考查居多。通過對近幾年的考題研究發現,和定最值的題型特征比較明顯,解題思路相對固定,所以考生一定要將其掌握。在此,小編為大家重點介紹如何求解和定最值這類題型。
題型特征
示例
29臺電腦分給5個部門,每個部門分得的電腦數量互不相同,問分得的電腦最多的部門最少分得多少臺電腦?
通過示例,在幾個量和一定的情況下,求某個量的最大值或最小值,這種題型我們稱之為和定最值。顯然,這種題型的題干描述簡單明了,題型特征容易識別。那么此類題目如何快速精準作答?我們繼續往下看。
解題原則
求某個量的最大值,就讓其他的量盡可能小;求某個量的最小值,就讓其他的量盡可能大。
題目演練
例1
某連鎖企業在10個城市共有100家專賣店,每個城市的專賣店數量都不同。如果專賣店數量排名第五多的城市有12家專賣店,那么專賣店數量排名最后的城市,最多有幾家專賣店?
A. 2 B.3 C.4 D.5
【參考解析】C。題干中10個城市共有100家專賣店,即10個量和一定,所求為排名最后的最大值,這就是和定最值問題。求排名最后的城市最多有幾家專賣店,則使其他城市盡可能少即可。由題干可知第五多的數量確定為12,那么也就可以確定第四到第一的依次為13、14、15、16家。而其余的量無法直接確定,結合題干每個專賣店的數量不同,可知第九多的再少也不能比排名最后的少,最小應是比排名最后的多一家。同理,第八多的比第九多的多一家,以此類推……那么我們可以假設排名最后的城市為X,因此第九到第六依次為X+1、X+2、X+3、X+4,根據總共100家就可以列以下方程:

例2
植樹節來臨之際,120人參加義務植樹活動,共分成人數不等且每組不少于10人的六個小組,每人只能參加一個小組,則參加人數第二多的小組最多有多少人?
A.32 B.34 C.36 D.38
【參考解析】C。題干中描述120人參加植樹活動,也就表明和是一定的,求參加第二多的小組最多有多少個人,要求此量最多就要使其他量盡可能少。由題干可知,每組不少于10人,那最少的小組最少就是10,又因為每組人數不同,所以第五到第三依次確定為11、12、13,而第一多的不能直接確定,但再少也不能比第二的少,若假設第二多的為X,那第一多的就是X+1。因為和是120,所以我們就可以列方程:
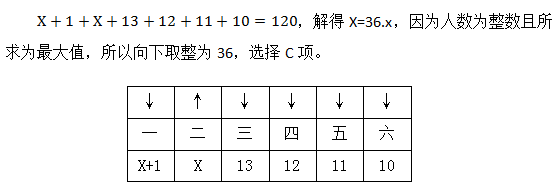
和定最值問題作為數量關系必須掌握的內容,考查的題型相對穩定,解題方法也主要是大家熟知的方程法。但還是需要注意以下兩點:一是排序的主體是否可以相同,一般考查都是不相同的,如果相同則在寫其他數據時就需要注意。二是最后解方程解出來的結果如果不是整數,應該如何取舍。牢記問最多向下取整,問最少向上取整。
最后,小編希望通過本次學習,大家能夠掌握這種題型。
 行測備考提醒
行測備考提醒 行測技巧還沒掌握?掃碼回復“咨詢老師”
行測技巧還沒掌握?掃碼回復“咨詢老師”


點擊分享此信息:
 相關文章
相關文章





