2025年云南公務員考試行測技巧:極值問題之一元二次函數求極值
 更多行測技巧與方法掃碼獲取
更多行測技巧與方法掃碼獲取
 云南省考行測數量關系技巧方法案例
云南省考行測數量關系技巧方法案例
極值問題之一元二次函數求極值
極值問題是一類經常出現的考點,考查頗為靈活。其中,利用一元二次函數求極值的題目較為典型。提到一元二次函數大家應該都不陌生,我們都知道其函數圖像為一條拋物線,且開口可能向上也可能向下,當開口向上時,函數有極小值;當開口向下時,函數有極大值。
但不管是哪種情況,函數總是對稱的,所以必然會在對稱軸位置處取得極值。那么對稱軸怎么求呢?我們可以令函數等于0,得到函數圖像與x軸的兩個交點,利用函數圖像的對稱性,找到兩個交點的正中間值,即為對稱軸的位置。下面讓我們來一起做兩道題加深一下理解:
例1、廠家生產銷售某新型節能產品,產品生產成本是168元,銷售定價為238元,一位買家向該廠家預定了120件產品,并提出如果產品售價每降低2元,就多訂購8件。則該廠家在這筆交易中所能獲得的最大利潤是( )元。
A.17920
B.13920
C.10000
D.8400
【解析】C。由題目所給信息,我們知道所求為總利潤的最大值。又因為總利潤=單件利潤×銷售量,所以需要把單件的利潤以及銷售量分別表示出來。具體來看,每一件產品的利潤為238-168=70(元),售價每降低2元,利潤也會跟著降低2元,所以在這不妨假設售價降低了x個2元,對應單件的利潤應表示為(70-2x)元;原銷售量為120件,并且售價每降低2元,銷售量就會增加8件,因此銷售量應表示為(120+8x)件。故總利潤為(70-2x)×(120+8x)元。所求為最大利潤,即這個函數的極大值。
在這里我們可以利用一元二次函數圖像的對稱性來求解,先讓函數的值等于0,即令:(70-2x)×(120+8x)=0,解得:x1=35或x2=-15。由其對稱性可知,x1和x2必關于對稱軸對稱,換言之,函數圖像的對稱軸正好位于x1和x2的正中間,即函數的對稱軸為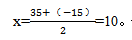 也就是說當x=10時,能獲得最大利潤。代入原函數,最大利潤為(70-2×10)×(120+8×10)=10000(元),故選C。
也就是說當x=10時,能獲得最大利潤。代入原函數,最大利潤為(70-2×10)×(120+8×10)=10000(元),故選C。
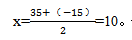 也就是說當x=10時,能獲得最大利潤。代入原函數,最大利潤為(70-2×10)×(120+8×10)=10000(元),故選C。
也就是說當x=10時,能獲得最大利潤。代入原函數,最大利潤為(70-2×10)×(120+8×10)=10000(元),故選C。 例2、某木苗公司準備出售一批木苗,如果每株以4元出售,可賣20萬株,若木苗單價每提高0.4元,就會少賣10000株。那么,在最佳定價的情況下,該公司的最大收入是多少萬元?
A.30
B.60
C.90
D.100
【解析】C。題目所求為最大收入,而收入=單價×銷售量,因此我們需要把單價和銷售量分別表示出來。先來看單價,單價為4元,設提高了x個0.4元,則單價=(4+0.4x)元;銷售量為20萬株,單價每提高0.4元,銷售量便減少1萬株,所以銷售量=(20-x)萬株。
因此收入=(4+0.4x)×(20-x)萬元,所求的收入最大值就是求這個一元二次函數的極大值。可以利用函數的對稱性來求解。令:(4+0.4x)×(20-x)=0,解得x1=-10或x2=20,由其對稱性可知,x1和x2必關于對稱軸對稱,則函數的對稱軸為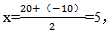 ,即當x=5時,收入最大,最大收入為(4+0.4×5)×(20-5)=90(萬元),故選C。
,即當x=5時,收入最大,最大收入為(4+0.4×5)×(20-5)=90(萬元),故選C。
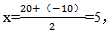 ,即當x=5時,收入最大,最大收入為(4+0.4×5)×(20-5)=90(萬元),故選C。
,即當x=5時,收入最大,最大收入為(4+0.4×5)×(20-5)=90(萬元),故選C。 以上就是關于一元二次函數求極值的題目,希望大家能夠借助上述題目把這個知識點搞懂、吃透。
 行測備考提醒
行測備考提醒 行測技巧還沒掌握?掃碼回復“咨詢老師”
行測技巧還沒掌握?掃碼回復“咨詢老師”


點擊分享此信息:
 相關文章
相關文章





